Crossword Compiler in Rust

The plan for the crossword compiler is to make an easy-to-use tool for someone to enter a list of crossword clues and their answers, and then my program will arrange the answers into a grid and output a neat PDF containing the empty grid and the numbered clues. There are existing tools to do this, but I’m yet to find one with all the settings I want, such as the ability to specify that a clue must be a “Down” clue (essential for a cryptic crossword).

Why Rust?

Rust is pretty awesome. The main appeal is that it runs as fast as C but is much easier to write, has a useful set of tools to aid development and handles memory in a much safer way. In terms of tools, cargo is a really nice tool that gives you simple commands to compile your code, run it, run tests etc.

I learnt Rust using The Book and then was keen to have a project to force me to learn more complicated ideas and get used to setting up testing, code coverage etc.

Genetic algorithms

I thought this would be an ideal project for a genetic algorithm. It turns out that a genetic algorithm isn’t actually ideally suited to this problem, which I’ll discuss later, but it did sort of work.

The idea of a genetic algorithm is to start with a bunch of random solutions, and iteratively combine these together, and mutate them to eventually reach a better solution. In this case, I started with grids consisting of single words, and then used the following types of moves to attempt to improve the solutions. Many of the changes would not be an improvement, but these sub-optimal solutions will get removed at the end of each round.

Types of moves:

• Split grid in half
• Add random word
• Prune leaves from grid
• Merge two grids together

Grid scoring:

• Proportion of cells that are filled (better if most cells are filled)
• How square the grid is (prefer grids that are square rather than e.g. tall and thin)
• Proportion of intersections (prefer grids where many cells are intersections between two clues)
• Number of words placed (eventually insist that all words are placed)
• Number of cycles (this makes the grid feel more like a single unit)

The basic plan was to alternate between (1) generating more solutions and (2) reducing the list to the best solutions. I decided to refine (2) to keep not just the best solutions, but to have a “varied” list of the best solutions. Essentially, I perform a greedy search through the solutions, picking the highest scoring solution available. Then I multiply the score of the remaining solutions by (1-similarity) to the newly chosen solution. This results in a list of good solutions, but where they are not all just essentially copies of the same one grid, but with minor varations.

This essentially worked, but I had planned the approach based on the move of merging two grids together (which I call recombination) but this is unlikely to be possible at all with any two random grids (because they might well both already have placed the same word) and even if the two grids can be merged, they are unlikely to merge together in a particularly helpful way.

Graphs!

I love graph theory, so I was delighted to spot that crosswords can be represented as graphs and that this representation offers some easy ways to calculate some of the scoring properties of the grids, such as number of cycles, number of intersections etc.

Each word is a node, and an edge is added between the word nodes if the two words intersect. An example is shown below.

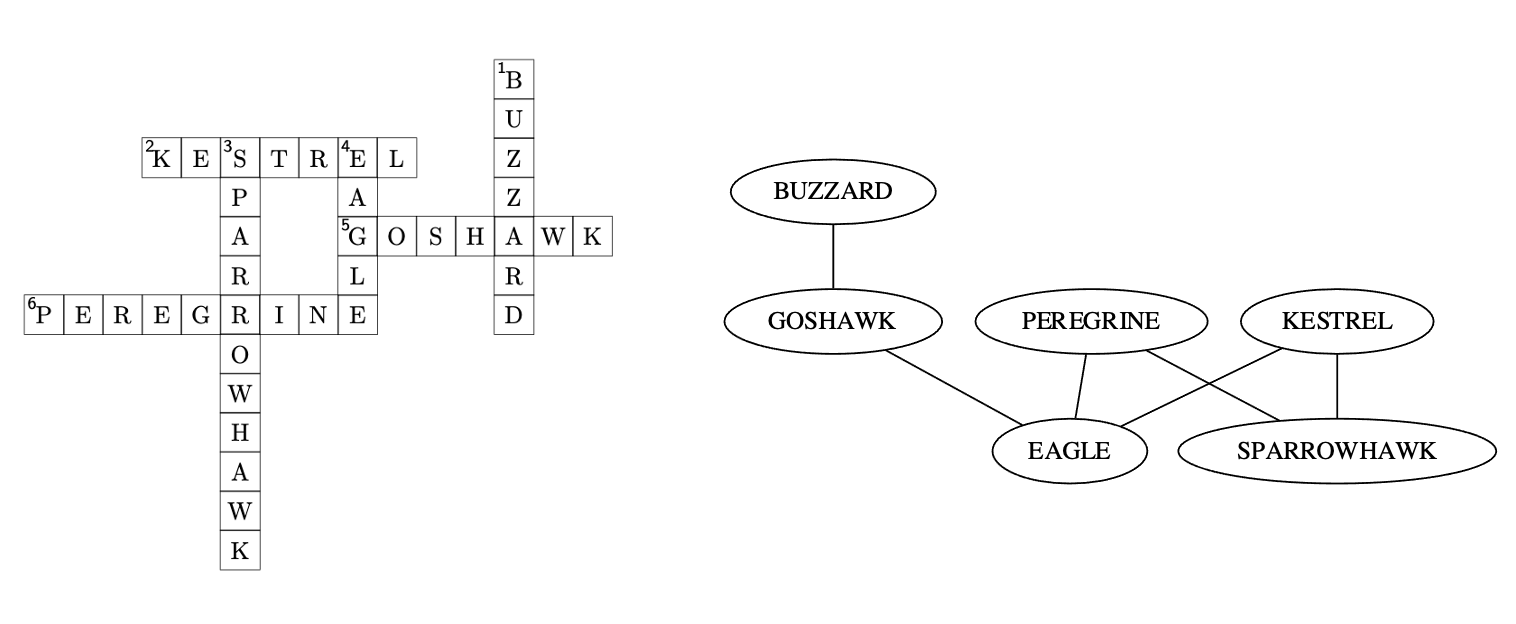
I use the graph representation for the following calculations:

• Connectivity - if the graph is connected, the crossword is connected.
• Number of cycles - again, the number of cycles in the crossword is the same as the number of cycles in the graph.
• Similarity between grids - the adjacency matrix of the graph offers an easy way to measure similarity between two grids, which is independent of rotation and translation.

Potential improvements

Overall, it was a really helpful project to get me started with Rust. I had hoped that I would be able to give the program a list of words from a real crossword (e.g. the Guardian cryptic crossword) and it would happily iterate and eventually return the “real” grid i.e. the actual optimal solution. The solutions were often fairly good, but never close to the optimal.

I started working on a web interface using rocket, but it needs quite a bit of work to make it really user-friendly. I also need to find a place to host it. Pythoneverywhere will probably work, despite the name…

If I revisit this problem I think I will use a more deterministic approach, exploring the space more completely and systematically. I’d love to be able to guarantee reaching the optimal solution when it exists (like the perfect grids from “real” crosswords) but still be able to provide “good” grids for more random collections of words. I dismissed this approach initially because I assumed that it would be faster to search in a greedier/more random way but since this hasn’t yielded results I think it is worth searching more derministically, and may end up being just as fast computationally.